Material Nonlinearity: Hardening Laws
Description
Hardening models describe the change of yield surface due to plastic strain accumulation.
-
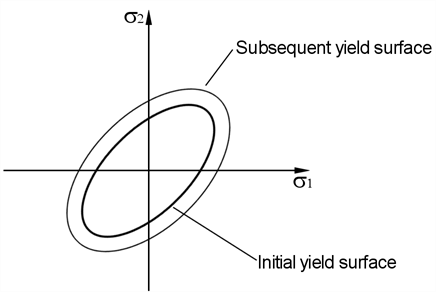
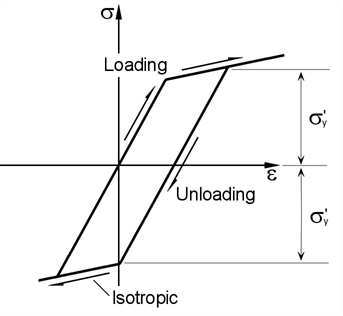
Isotropic
The yield stress is a function of the equivalent plastic strain and the yield surface expands while its centre remains fixed.
Isotropic hardening is available for beam, plate and brick elements.
-
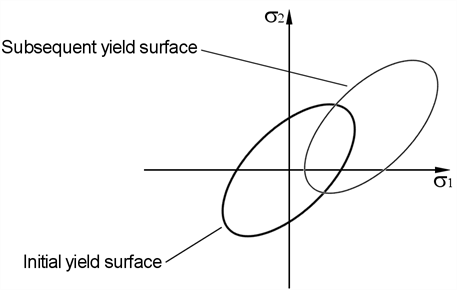
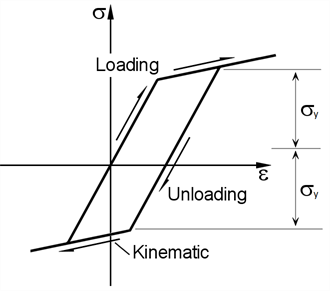
Kinematic
The centre of the yield surface is a function of the plastic strain and moves in stress space while the size and shape of the yield surface remains unchanged.
Kinematic hardening is available for beam elements only.
-
Takeda
This is a special case of a mixed hardening model, which combines isotropic and kinematic hardening models. The model was developed specifically for reinforced concrete members under repeated dynamic loading/unloading.
Takeda hardening model is available for beam elements only.
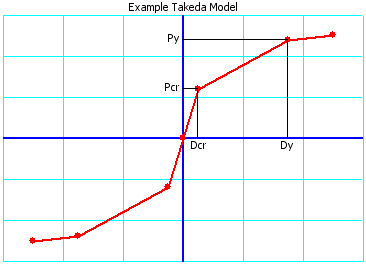
A valid Takeda model curve is trilinear and passes through the origin (0, 0). There are two gradient changes in the curve:
- The cracking point [Pcr (cracking load), Dcr (cracking deflection)]
- The yield point [Py (yield load), Dy (yield deflection)]
An example curve is shown below:
Literature
Takeda, T., Sozen, M.A. & Nielsen, N.N. 1970, "Reinforced Concrete Response to Simulated Earthquakes", Journal of the Structural Division, Proceedings of the American Society of Civil Engineers, vol.96, no. ST12, December.
See Also