SOLVERS Parameters: EIGENVALUE

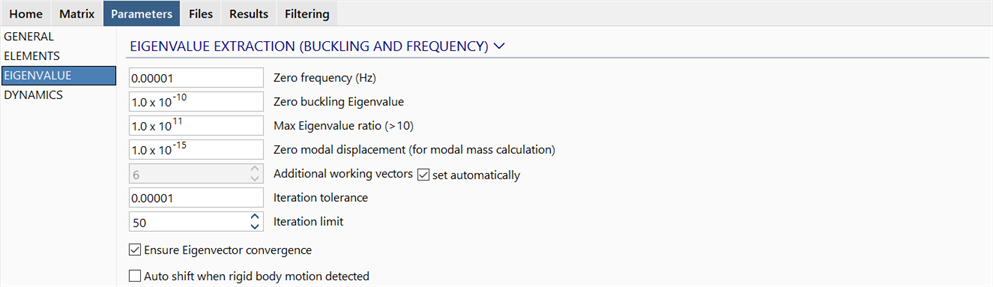
Description

Sets the parameters that apply to the eigenvalue extraction algorithm used by the Natural Frequency and the Linear Buckling solvers.

Zero frequency (Hertz)

This is the limiting value below which a natural frequency is regarded as zero. A zero frequency usually means a rigid body mode (or a free floating structure or component of a structure).

Zero buckling eigenvalue

This is the limiting value below which a buckling load factor is regarded as zero. A zero eigenvalue in a buckling analysis indicates that some part of the structure has zero stiffness. This is an indication of a rigid body mode or that the structure has a mechanism.

Max eigenvalue ratio (>10)

Sets a limit between the smallest and the largest eigenvalues within a sub-space iteration. An eigenvalue will not be considered as zero unless the maximum eigenvalue in the set exceeds this ratio. The bigger the ratio, the more vectors are retained within the sub-space.

Zero modal displacement (for modal mass calculation)

This is the limiting value below which an eigenvector is assumed to be a zero vector. During the calculation of modal mass, the eigenvector is normalised relative to the maximum displacement component in the vector. If the maximum displacement component is smaller than this value, the eigenvector is not normalised and it is assumed to be the zero vector

Additional working vectors

This is the number of additional base vectors to be included in the sub-space iteration procedure of the eigenvalue extraction algorithm.

By default, the solver extracts more modes than requested by the user, but only reports the user requested modes. It does this to help improve the convergence of the higher modes. By increasing this parameter further, the convergence of higher modes can be further improved and solutions are usually obtained in fewer iterations, although each iteration will take longer to complete.

set automatically

If set, an appropriate number of additional base vectors is automatically determined by the solver based on the size of the model and the number of modes requested.

Iteration tolerance

This parameter is used to check the convergence of the eigenvalues, an optionally also the eigenvectors. An eigenvalue is regarded as converged when the relative difference between two successive iterations is less than this value. The relative difference is defined as:

where

is the eigenvalue at the current iteration

is the eigenvalue at the previous iteration

A similar measure is used for the eigenvector convergence, except that the ratio is calculated as the norm of the difference in the eigenvector between successive iterations and the norm of the current estimate of the eigenvector.

Iteration limit

This is the maximum number of iterations allowed for the eigenvalue extraction procedure. If all the requested eigenvalues have not converged within this limit, the solution stops and the current eigenvectors and eigenvalues are saved to the results file.

Unconverged modes should not be included in analyses based on mode superposition (such as harmonic response, spectral response and linear transient dynamic with mode superposition) as they may lead to unexpected (erroneous) results. A mass participation ratio greater than 100% in spectral response analysis is usually the result of non converged eigenvectors (i.e., mode shapes).

Ensure eigenvector convergence

If set, the solver keeps iterating until each requested eigenvalue + eigenvector (mode shape) pair are both converged.

If not set, the solver iterates only until all the eigenvalues have converged. At that point it checks the eigenvector convergence and issues a warning if any are not converged. Using unconverged mode shapes for downstream applications such as for mode superposition in the Harmonic Response, Spectral Response and Linear Transient Dynamic solvers can have detrimental effects on results accuracy.

Auto shift when rigid body motion detected

If set, and the solver detects rigid body motion, a small shift is used in the eigenvalue extraction procedure. This allows for the calculation of both rigid body modes and deformational modes, depending on the number of modes requested (in a general 3D problem, there will be six zero, or rigid body modes, so the first deformational mode will be mode 7). Depending on the problem, some adjustment of the shift value may be required to solve models that are not restrained.