Entities: Consistent vs Lumped Load

Description

In finite element analysis, the deformation of a structure is described through the displacements at a finite number of nodes. From the node displacements, the displacement fields over connected elements are expressed using element shape (or interpolation) functions.

Similarly, when loads are applied to the interior of the elements, instead of directly to the nodes, a conversion is required to convert these element loads to nodal loads. Two of the commonly used conversion methods are the lumped (non-consistent) and the consistent approaches. An example of the nodal forces/moments for the case of a beam element with a uniformly distributed load is shown below:

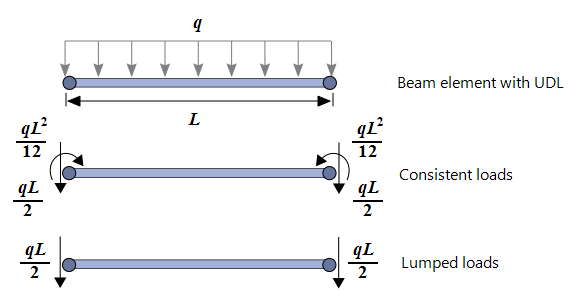
The lumped approach tends to be an intuitive one whereby the total force on an element from a distributed load is simply divided by the number of nodes on the element and applied to each node. For elements such as beam and linear plates, this approach can produce reasonably accurate load distributions, particularly as the element is refined. However, this does not generally apply to higher order elements (e.g., Hexa20 brick element) as the load proportions at the mid-side nodes are usually different to the load proportions at the corner nodes.

The correct (or consistent) distribution of load requires an integration of the element shape functions. That is, for a load density vector applied over an element (face or body), the nodal forces are calculated from the element shape functions, , as

For beam and plate/shell problems, the above expression may yield a load vector containing both force and moment terms for a distributed load.