Creep: Concrete Creep and Shrinkage - Hyperbolic Law

Description

Defines creep data parameters according to the hyperbolic creep law.

The implementation of the hyperbolic creep law in Straus7 is in a generalised form, which therefore makes it amenable to many commonly used concrete design codes such as ACI 209R-92 and CEB FIP Model Code 1990.

Toolbar Functions

See LAYOUTS: Creep.

Creep Tab

Within the usual working stress range, the creep strain is approximately proportional to the applied stress . Due to the initial elastic strain also being proportional to the applied stress it has been found useful to develop a stress-independent quantity which is referred to as the creep coefficient:

As approaches infinity, the creep coefficient is assumed to reach a limit value where

The final or ultimate creep coefficient is a useful measure of the capacity of concrete to creep.

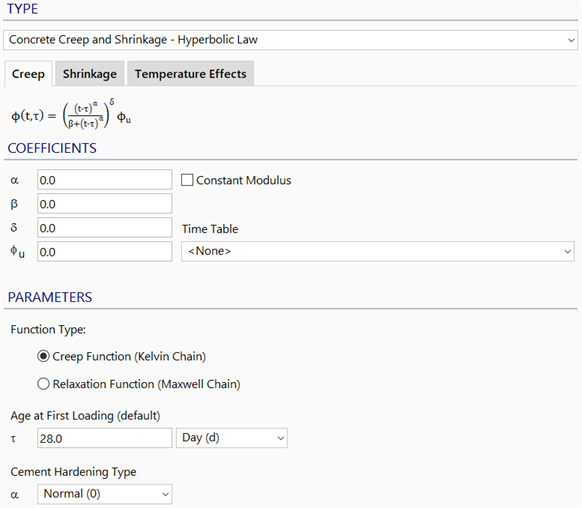
Coefficients and Parameters

Defines the development of the concrete creep coefficient with time according to:

where

is time;

is the age of concrete at first loading;

is the exponent of the duration of loading ;

is a parameter that influences the rate of development of creep strain;

is the function exponent; and

is the ultimate creep coefficient (or the limit value of creep coefficient as time approaches infinity). To take into account the ageing effects of concrete, a Factor vs Time table can be assigned to this ultimate creep coefficient.

Constant Modulus

If set, the creep strain is calculated based on a constant modulus defined in the material property dialog. If this option is not set and a Modulus vs Time table has been selected in the material property dialog, the creep strain will be calculated based on a time varying modulus. For instance, ACI 209R-92 requires the use of a variable modulus for calculating the creep strain whilst the CEB-FIP Model Code 90 does not.

Function Type

Specifies the type of function that is used in curve fitting creep data generated by the hyperbolic law. Two types of function are available:

Creep Function (Kelvin Chain)

Creep strain versus time data is generated by applying a unit stress at various ages of loading to the hyperbolic law provided. This data is then curve fitted according to parameters set under the Solver Parameters Tab: Creep (see SOLVERS Parameters: CREEP) using a Concrete Creep: Generalised Kelvin Chain.
Relaxation Function (Maxwell Chain)

Stress vs time data is generated by applying a unit strain at various ages of loading to the hyperbolic law provided. This data is then curve fitted according to parameters set under Solver Parameters Tab: Creep (see SOLVERS Parameters: CREEP) using a Concrete Creep: Generalised Maxwell Chain.

Age at First Loading

Specifies the age of the concrete at the beginning of the analysis.

Cement Hardening Type

The cement hardening type can be set to Slow, Normal or Rapid.

The effect of these cement types on concrete creep behaviour can be taken into account by modifying the ages of loading during the curve fitting of the hyperbolic law to either a Concrete Creep: Generalised Kelvin Chain (Creep function) or a Concrete Creep: Generalised Maxwell Chain (Relaxation function). The ages at loading are modified according to:

is the age of concrete (in days) at loading adjusted due to curing temperature effects.

is an exponent which takes a value of:

–1 for slow hardening cement
0 for normal hardening cement
+1 for rapid hardening cement

is the effective age of concrete (in days).

Shrinkage Tab

The Shrinkage tab specifies the concrete shrinkage properties.

See Concrete Creep and Shrinkage: Shrinkage.

Temperature Effects Tab

The Temperature Effects tab specifies properties that account for temperature effects on the creep, shrinkage and cement curing of concrete.

See Concrete Creep and Shrinkage - Temperature Effects.