SOLVERS Parameters: CREEP

Description

Sets creep parameters that apply to the Quasi-static and Nonlinear Transient Dynamic solvers.

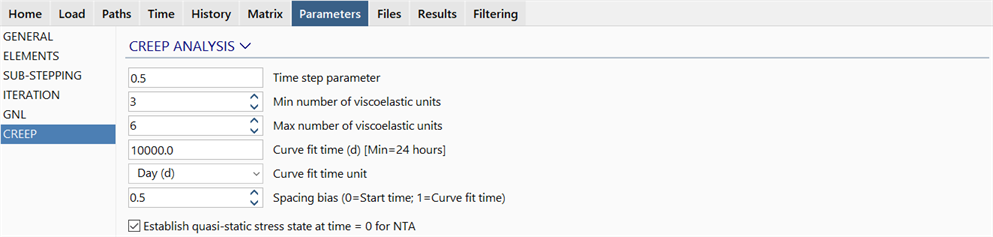
Time step parameter

The time step parameter controls the time integration scheme for a numerical creep solution. The default value, 0.5, corresponds to an implicit trapezoidal scheme where the creep strain increment is determined from the creep strain rate corresponding to the mid-point of the time interval.

Min/Max number of viscoelastic units

When Creep: Concrete Creep and Shrinkage - Hyperbolic Law or Creep: Concrete Creep and Shrinkage - User-Defined are used, a curve fitting procedure is carried out to find an equivalent viscoelastic chain that represents the creep data entered in the property set. The Min and Max number of viscoelastic units settings provide a lower and upper bound guide for the solver. The solver may still end up with many more than the max number of units.

Curve fit time (d) [Min=24 hours]

When Creep: Concrete Creep and Shrinkage - Hyperbolic Law is used, the curve fit time sets the time duration over which the hyperbolic law is evaluated for curve fitting (i.e., to find the equivalent viscoelastic chain to represent the creep data).

The curve fit time affects the accuracy of the response in that the curve fit is a best-fit curve over the chosen time interval (the Curve fit time). If higher accuracy is required over a specific period (e.g., the initial period), a shorter curve fit time will generate a more accurate fit over the initial period, at (possibly) the expense of a less accurate fit over the longer period.

If the Creep Function setting is used in the creep definition, creep strain vs time data is generated by applying a unit stress at various ages of loading for the duration of the curve fit time to the hyperbolic law provided. This data is then curve fitted using a Concrete Creep: Generalised Kelvin Chain model.

If the Relaxation Function setting is used in the creep definition, stress vs time data is generated by applying a unit strain at various ages of loading for the duration of this curve fit time to the hyperbolic law provided. This data is then curve fitted using a Concrete Creep: Generalised Maxwell Chain model.

Curve fit time unit

Defines the time unit for the Curve fit time.

Spacing bias (0=Start time to 1=Curve fit time)

Provides a hint to the solver for curve fitting the Creep: Concrete Creep and Shrinkage - Hyperbolic Law and Creep: Concrete Creep and Shrinkage - User-Defined to find the equivalent viscoelastic chain to represent the creep data. The default value, 0.5, corresponds to a uniform spacing of the relaxation/retardation times of the viscoelastic units in a logarithmic time scale. A lower value will result in more fit points being inserted during the initial creep response, while a higher value will result in more fit points being inserted during the final creep response (i.e., more fit points closer to the end of the Curve fit time).

Establish quasi-static stress state at time = 0 for NTA

If set, the initial state of stress is established based on the static loads at time zero. The stresses due to the static loads are then used to calculate the initial creep strain rates at the commencement of the transient dynamic analysis.

If not set, loads are assumed to just start at time zero, and therefore the initial creep strain rate will be zero. The creep strain rate will then develop as the stress in the model develops.

In a nonlinear transient dynamic analysis, if a model is not restrained and is relying on its inertia for stability, this option cannot be used because the quasi-static solution will be singular. To avoid a singular quasi-static solution, a nonlinear static initial condition can be specified to establish the initial creep rate (see SOLVERS Home: Initial Conditions (Transient Dynamic)). If the initial creep rate can be considered to be negligibly small, and the initial state of stress can be ignored, no initial conditions are required and the solution can proceed by clearing the option.

In the Quasi-static solver, the initial stress state is always established before the time stepping solution can proceed. If a nonlinear static result is used as initial conditions (see SOLVERS Home: Initial Conditions (Static)), those results are used to calculate the initial creep rate. If no initial conditions are specified, the Quasi-static solver inserts an additional instantaneous result case denoted at time zero from which the initial creep rate is calculated. This is effectively a nonlinear static analysis based on the initial loads in the Quasi-static solver.