Materials: Metal Creep

Description

Creep is defined as the time-dependent, thermally assisted, deformation of a stressed or loaded body. It usually becomes significant over a prolonged period of load at temperatures above 0.3 , where is the melting point of the material.

Practical examples where materials are required to survive long periods under load at high temperatures include:

Aircraft engines: jet engines operate in extremely high temperatures, nearly 1000 °C, which can lead to creep deformation in regions of the structure or casing.
Power generation equipment: the constant centrifugal forces acting on turbine blades leading to creep deformation of the blades. Over time the blades may come in contact with the outer casing and ultimately fail.
Chemical, mining and oil industry equipment: pressure vessels in power plants, nuclear reactors and material processing facilities operate in an environment of superheated steam where creep can be a significant issue for these structures.

Design criteria for long operation under stress at high temperatures must guarantee that:

creep deformation does not cause excessive distortion over the planned service life.
creep rupture failure does not occur within the required operating life.

Uniaxial Creep

The first step in predicting the creep behaviour of a complex engineering component entails the development of uniaxial creep models.

The typical (creep) strain response with time for a uniaxial tensile specimen under constant load and at constant elevated temperature is shown in the figure below:

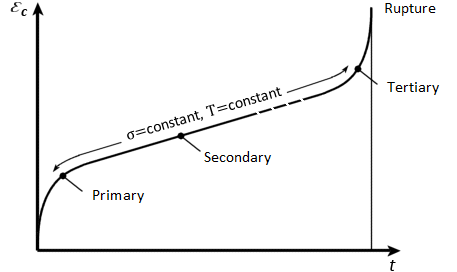
Many expressions have been proposed to describe the above creep curve. However, there is currently no all-embracing theory that can accommodate all situations or eventualities. With the creep strain being dependent on stress, , time, , and temperature, , the most general creep equation is:

In the development of the mathematical expressions for uniaxial creep laws, it has been found useful to describe the observed creep curves by referring to different regions of the curve. These different regions are distinguished by the creep strain rates observed during the development of the creep strain curve.

After the initial (elastic) strain on loading, the creep rate usually decays during the primary stage until an apparent constant creep rate is reached during the secondary stage, after which the creep rate increases again during the tertiary stage which leads to rupture.

Multiaxial Creep

In order to predict the creep behaviour of engineering components, it is necessary to generalise the various uniaxial creep theories to include multiaxial stress states.

The foundations of multiaxial creep laws are very closely aligned to the concepts proposed in classical plasticity.

The uniaxial creep laws may be extended to the multiaxial case through the introduction of effective (or equivalent) quantities, such as the effective stress,, and effective creep strain rate, .

For example, if the power law for secondary creep is assumed, then:

Similarly, other uniaxial models may also be used and extended to the multiaxial case in this manner.

Straus7 uses von Mises stress to calculate the effective creep strain rates.