Global: Define Toroidal UCS
Description
Defines a toroidal coordinate system (UCS) (see Global: Define UCS).
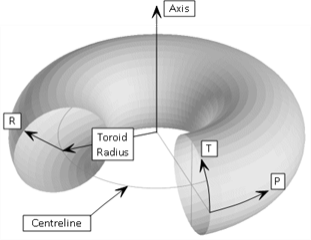
Toroidal coordinate systems use the coordinates R, T and P (radius, theta and phi) to define the position of a point. R is a distance measured from the toroidal centreline, whereas T and P are angles. P is measured along the toroidal centreline. A rotation about the axis of the toroidal UCS, using the right-hand rule, defines the direction of positive P.
At any location (R,T,P), the respective R, T and P direction vectors are mutually perpendicular.
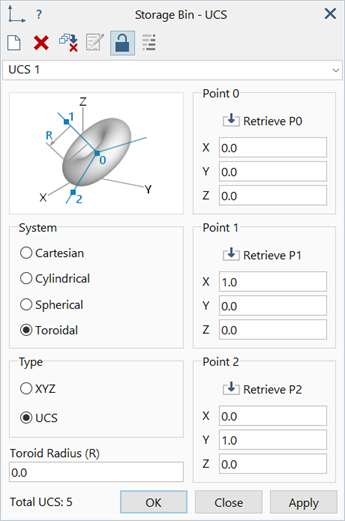
Dialog
Type
Method used to position and orientate the toroidal UCS.
-
XYZ
A single point (Point 0) defines the origin of the toroidal UCS.
The toroidal centreline is a circle of fixed radius on the global XY plane, centred at Point 0.
The axis of the UCS is parallel to the global Z axis.
The P=0 position on the toroidal centreline is located on the line parallel to the global X axis, passing through the origin of the toroidal UCS.
Point 1 and Point 2 are implicitly defined.
-
UCS
Three points (Point 0, Point 1 and Point 2) define an arbitrarily orientated toroidal UCS.
The origin is located at Point 0.
The axis of the UCS is directed from Point 0 to Point 1.
The toroidal centreline is a circle of fixed radius on the plane whose normal is the toroidal axis.
The P=0 position on the toroidal centreline is located on the line passing through the origin of the toroidal UCS and Point 2.
Toroid Radius
Distance from the origin to the toroidal centreline. The coordinate R in (R,T,P) is a distance measured from the toroidal centreline.
Point 0 / Point 1 / Point 2
Three points used to position and orientate a toroidal UCS.
Coordinates of points may be retrieved from the model by clicking a node, vertex or grid point, or by explicitly typing the values into the edit boxes.
See Also