Special Topics: Damping

Description

Damping is a term used to describe the energy loss in a dynamic system. There are many mechanisms responsible for damping, including material damping, friction at contact surfaces, and so on. In Strand7, damping is represented by different linear damping models. Three models are available:

Rayleigh damping,
modal damping, and
viscous damping.

Each of these models proposes a way of defining the global damping matrix, , in the following matrix equation of motion,

which relates the time derivatives of nodal displacement , with the forcing vector .

Different solvers support different forms of damping as summarised below.

Natural Frequency Solver

The Natural Frequency solver calculates the undamped natural frequencies and mode shapes of a structure. It does not consider damping when calculating these results. However, the Natural Frequency solver can be used to calculate effective modal damping ratios for the modes using material damping ratios defined in the element property data Common Properties: Damping (Damping Ratio (NFA)).

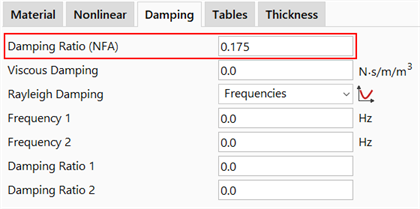
Damping Ratio (NFA) is a dimensionless value,, representing the ratio of damping to that of critical damping ( represents critical damping). Different values can be defined for different properties in a model.

If these ratios have been defined for one or more element properties, and Calculate Mode Participation has been set in the solver (SOLVERS Home: Mode Participation),

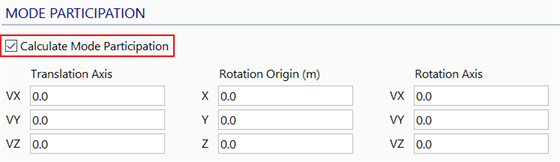
the modal damping ratios will be produced and listed in the solver log file (Results Interpretation: Solver Log File).

These ratios can then be extracted from the natural frequency solution file and used as modal damping ratios in the Harmonic Response and Spectral Response solvers. Values are retrieved from SOLVERS: Modes.

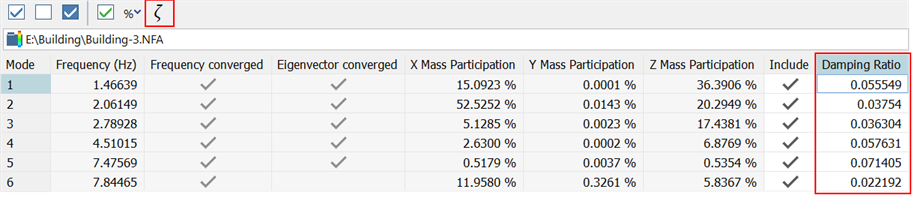
This functionality is useful where the structure has material properties with varying damping characteristics: for example, soil will have different damping behaviour to concrete, so the modal damping ratio of a concrete structure resting on a soil foundation will depend on the deformation (i.e., the mode) and the damping ratio of each structural component or material. The different property data for the different materials can be assigned different damping ratios.

Linear Transient Dynamic and Nonlinear Transient Dynamic Solvers

These solvers offer the option of ADDED DAMPING with either Rayleigh or Property as selections, in addition to None.

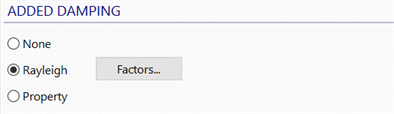
The reason it is called ADDED DAMPING is that damping may already be included due to the presence of Spring-Damper elements and/or Translational Node Damping attributes; these add damping, defined in physical units (e.g., N.s/m), and are always assembled into the global damping matrix for linear and nonlinear transient dynamic analysis. Additional damping can be added using one of the Rayleigh or Property options offered by these solvers.

If Rayleigh is selected, a damping matrix based on the global mass and stiffness matrices of the system, together with the damping factors defined here, is assembled as described in the Rayleigh Damping section below.

If Property is selected, two types of additional damping can be added depending on the data defined in the element property: Viscous Damping, which is defined in physical units per unit volume (e.g., N.s/m/m³), and/or Rayleigh Damping, which is based on the stiffness and mass matrices of elements that reference the property, together with the Rayleigh factors defined in the property.

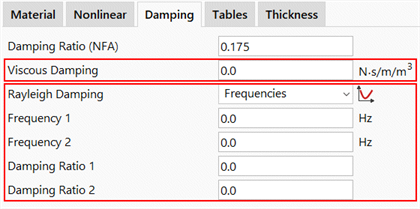
The advantage of the Property option for Rayleigh damping, compared with the global matrix option, is that the Property option allows for different damping characteristics to be assigned to different parts of a structure based on the material. This is not possible if the Rayleigh damping matrix is assembled based on a single set of factors that scale the global mass and stiffness matrices.

Harmonic Response Solver

This solver offers the option of DAMPING with either Rayleigh or Modal as selections.

If Modal is selected, a modal damping ratio is defined for each included mode of the natural frequency solution via SOLVERS: Modes. Each modal damping ratio is a dimensionless value,, representing the ratio of damping to critical damping ( for critical damping), and is used in the modal superposition as described in Modal Damping, below.

If Rayleigh is selected, a modal damping ratio is calculated for each natural frequency using the Rayleigh relation (see below). This value of damping ratio is then used for modal damping in the same way as the Modal option.

Spectral Response Solver

This solver offers the option of DAMPING with either Rayleigh or Modal as selections.

SPECTRUM Type = Response

The two options, Rayleigh and Modal, are used to define modal damping ratios in the same way they are defined for the Harmonic Response solver, described above. However, for Response Spectrum analysis, damping ratios are not used to calculate the modal response of the structure, they are used only to combine the modal responses to calculate the CQC (Complete Quadratic Combination) result case (see Solvers Background: Spectral Response).

SPECTRUM Type = PSD

The two options, Rayleigh and Modal, are used to define modal damping ratios in the same way they are defined for the Harmonic Response solver, described above. For the PSD Spectrum, the modal damping ratios are used to calculate the modal responses of the included modes. Similarly to Response Spectrum analysis, the damping ratios are then used to combine the modal responses to calculate the CQC (Complete Quadratic Combination) result case (see Solvers Background: Spectral Response).

Discrete Spring-Damper elements and Translational Node Damping attributes

These are considered only in the Full SystemSOLVERS: Linear Transient Dynamic Settings and SOLVERS: Nonlinear Transient Dynamic Settings. They are always considered in these solvers irrespective of the SOLVERS Home: Damping/Added Damping option.

Rayleigh Damping

Rayleigh damping, also known as proportional damping, is one of the most common models of damping used in finite element analysis. In this model, the damping matrix is assumed to be a linear combination of the stiffness and mass matrices as follows:

where

, and are damping, mass and stiffness matrices, respectively, and

and are the mass and stiffness proportional damping constants, respectively.

The relationship between and and the damping ratio, , at a frequency , is given by:

The constants and are often determined by defining the damping ratios, and , at two frequencies, and . Solving two simultaneous equations based on the above relationship yields:

Usually and are chosen such that they cover all the frequencies of interest in the design, with as the lowest and as the highest in the frequency range.

Rayleigh damping has two distinct components. The stiffness proportional damping, , which increases with increasing frequency, and the mass proportional damping, , which decreases with increasing frequency. This is shown in the following figure:

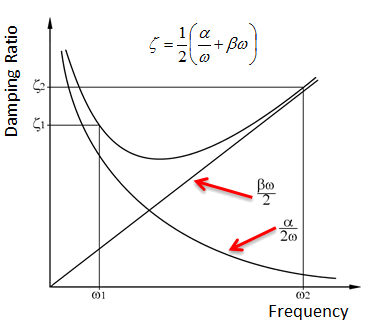
While Rayleigh damping tends to underdamp the structure over the frequency range between and , and overdamp the frequencies outside of this range, in most cases it provides an efficient and straightforward method of modelling damping in the system. When choosing the two frequencies at which the damping factors are to be specified, the frequencies should be as close as possible to the lower and upper limits of the frequency range of interest, to minimise error.

As Rayleigh damping consists of two independent terms, the mass term and the stiffness term, Strand7 allows for and to be specified directly (see SOLVERS Home: Rayleigh Damping), bypassing the need to define two damping ratios at two frequencies. This facility provides more flexibility for tuning the damping mechanism within a structure. As the mass term produces damping based on the rigid body velocity of an element (similarly to inertia forces generated by an accelerating mass), and the stiffness term produces damping based on the relative deformational velocity of nodes on an element (similarly to elastic forces generated by relative displacements acting on the stiffness matrix), it is possible to adjust these two damping contributions independently.

Modal Damping

Modal damping is another commonly used damping model. It allows the modal damping ratio to be defined independently for each vibration mode used in any analysis based on the modal superposition technique; this includes the Harmonic Response, Spectral Response and Linear Transient Dynamic (Mode Superposition) solvers.

The modal damping value for vibration mode i is often denoted by , and with modal damping included, the modal equilibrium equation is normally expressed in the following form:

where is the modal displacement, is the frequency, and is modal load.

The facility to define different modal damping ratios for different modes is useful in situations where different modes excite different materials or components in a complex structure. For example, a concrete structure sitting on a soil foundation will experience some modes where the movement is dominated by the structural deformation of the concrete, and other modes where the concrete structure moves as a rigid body on the soil foundation. In this case the concrete deformational modes could have a damping ratio of 5% (say) and the rigid body modes could have a damping ratio of around 10% - 20% (say).

Generally, modal damping is used in conjunction with experimental results; when the damping ratios are accurate, it provides a good damping model.

Viscous Damping

This property attribute, , defines a value of damping for the material in physical units (e.g., N.s/m/m³). This value is defined on a per volume basis similarly to mass density because it is integrated over the volume of the element to produce an element damping matrix, , in the same way as the element mass matrix is constructed. That is,

This element damping matrix is then transformed to the global system and added to the global damping matrix.

Due to the way this matrix is defined, its effects are similar to the effects of the mass proportional part of Rayleigh damping. The difference is only in the magnitude of the coefficients of the respective matrices as they are derived from different starting points.