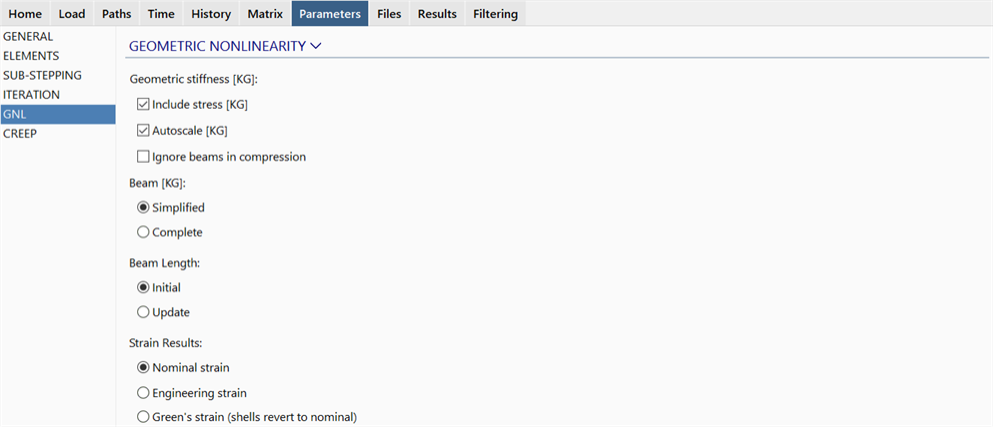
SOLVERS Parameters: GNL
Description
Sets variables that control the behaviour of analysis and results when geometric nonlinearity (GNL) is considered.
Include stress [KG]
If set, adds the element geometric stiffness matrix, [KG], to the global stiffness matrix.
This matrix accounts for the change in tangent stiffness in an element due to the presence of internal stress (e.g., the lateral stiffness of a bar increases when the bar is tensioned). This matrix mostly affects the convergence rate of a nonlinear geometry analysis. As the matrix does not take part in equilibrium calculations, it does not affect the results when those results are converged.
Autoscale [KG]
Since [KG] itself does not affect the results of a converged step, in some cases convergence can be more stable by not including the full effects of [KG], or by excluding it altogether. When the full [KG] is not included, the global stiffness matrix is no longer the true tangent stiffness, but this is acceptable within the context of the Modified Newton-Raphson algorithm used to solve such problems.
Ignore beams in compression
If set, [KG] is not added for beams in compression, and this can provide more numerical stability in some solutions. The reasons for this option are similar to those given for the previous two parameters.
Beam [KG]
When [KG] is added to a beam element, two options are available regarding its formulation:
-
Simplified
This option includes only the axial component of the geometric stiffness matrix and offers the best overall performance and stability for nonlinear geometry (GNL) solutions.
-
Complete
This option includes all terms in the geometric stiffness matrix and can achieve better performance in nonlinear geometry (GNL) solutions when there is significant twist-bend loading in beam elements.
Beam Length
In nonlinear geometry analysis, the beam length considered by the solver can be either the initial length or the current length. For small strain problems this setting has minimal effect on the solution. But if something like a telescopic arm needs to be modelled, the Update option should be used.
-
Initial
The initial length is used to evaluate length-dependent quantities and to assemble the stiffness matrix.
-
Update
The current length is used to evaluate length-dependent quantities and to assemble the stiffness matrix.
Finite Strain Definition
In geometry nonlinear analysis, strain results may be reported by choosing one of three definitions: nominal, engineering or Green's. These definitions are illustrated below for the one dimensional case where the initial length is , and the current length is
.
-
Nominal strain
Strain is interpreted as the ratio of the change in length over the current length:
-
Engineering strain
Strain is interpreted as the ratio of the change in length over the initial length:
-
Green's Strain (shells revert to nominal)
Strain is interpreted as:
This option gives a more mathematical measure of strain. It is the strain that is used internally by the solver during the iterations. The local strains are reported in the original undeformed coordinate system, as such, the display of local strain contours is meaningful only if the displacement scale is set to zero.
For plate/shell elements, nominal strain definition is used instead.
See Also