Special Topics: Equivalent Static Seismic Analysis
Description
Based on certain assumptions, the dynamic load in a seismic event can be approximated as an equivalent static load. This allows for the structural response to be determined by running a linear static analysis. Depending on the structure, this approach can be used as a simpler alternative to the more complex spectral response analysis (SOLVERS: Spectral Response Settings) or time history analysis (SOLVERS: Linear Transient Dynamic Settings, SOLVERS: Nonlinear Transient Dynamic Settings).
The equivalent static loads for the seismic event are assumed to act in the horizontal directions (i.e., in directions perpendicular to the direction of gravity) and are calculated according to the considerations described below.
The implementation in Straus7 is a general one, which therefore makes it applicable to virtually any national design code (for example, AS 1170.4 – Australian Standard, Structural design actions, Part 4: Earthquake actions in Australia).
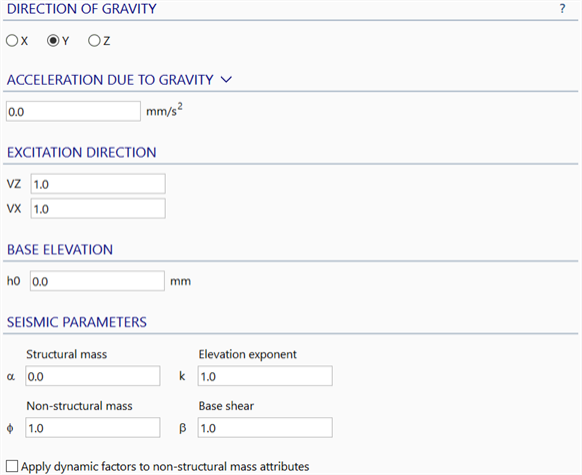
Seismic base shear
The horizontal equivalent static shear force, , acting at the base of the structure in the specified excitation direction can be expressed as:
where
is the total seismic weight of the structure due to gravity, and
is a factor, which may be related to the importance of the structure, the site factor for the foundation soil profile and so on, depending on the specific code requirements.
The base of the structure, as far as the model is concerned, includes any restrained nodes whose reaction forces contribute to .
Gravity load
The seismic weight, , on the structure is calculated as:
where
is the gravitational acceleration in the specified direction, always perpendicular to the base shear direction;
is the effective mass of the structure, which is a combination of the structural mass,
, and the non-structural mass,
; and
are non-dimensional combination factors, which are usually greater than zero and never negative.
Vertical distribution of horizontal seismic forces
The horizontal equivalent static force, , at node
is determined by the following equation:
where
is the seismic weight of node
such that
where
and
are structural and non-structural masses, respectively, at node
;
is the height of node
above the base (i.e.,
) where
is the vertical coordinate of node
, and
is the vertical coordinate of the base (Base Elevation);
is an exponent, which may take a unit value or can be related to the fundamental period of the structure, and
is the total number of nodes in the model.
The above effectively distributes the base shear resultant force, , over the structure as a function of height, to nodes that have mass.
Gravity and excitation direction
In addition to the above parameters, the magnitude and direction of the gravitational acceleration, together with the direction of the equivalent static force (the Excitation Direction), must be specified. The Excitation Direction entered is always normalised; it defines only the direction of the horizontal force, in the plane whose normal is the gravity direction (i.e., the magnitude of the force is not affected by the magnitude of the excitation direction).
See Also