Results Interpretation: Beam Taper

Description

The number of lengthwise integration points that the solvers use for the integration of tapered beams is set via the Common Properties: Sections. At each of these points, the section properties, including shear stress coefficients, are required before the solvers can be launched. If these properties have already been calculated, the solver will use the available data. For tapered beams with missing data, the calculation methods employed in the Special Topics: BXS Generator are used prior to launching the solvers to produce the required data. Once calculated, the data is stored with the model file to future use.

To avoid having to calculate missing data at solve time, the Utility: Tapers function can be executed. This will generate all the missing tapered beam property data.

The reason this property data may be missing for tapered beams is that once tapered, the beam cannot use the section properties defined in the property set. Those properties are calculated based on an untapered section. For different taper ratios on different beams, complete sets of property data need to be calculated, even if all the beams use the same cross sections. The application of a new taper ratio on a beam will usually mean that new data will be required.

Example

Tapered beam results are compared with a simple example using conservation of energy. The Elastic Strain Energy in a beam can be expressed as follows:

where is the Elastic Strain Energy;

is the internal bending moment varying along the beam;

is the Young's Modulus varying along the beam;

is the second moment of area about neutral axis;

is the total beam length;

is the variable length from one beam end.

If a loading is gradually applied onto a beam such that kinetic energy can be neglected, and it eventually causes the beam to displace in the same direction of loading, this physical load is said to be transformed into elastic strain energy stored internally in the beam. And therefore, the conservation of energy states that the work done by external load is equal to the internal energy stored at the state of equilibrium as follows:

thus,

where

is the applied load;

is the vertical deflection in the same direction of applied load.

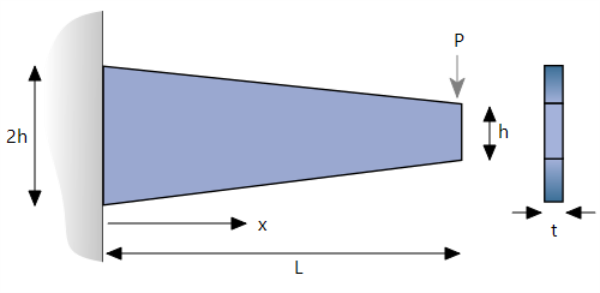
A simple symmetrically tapered cantilever beam is considered. The beam comprises of a solid rectangular cross section that has the second moment of area and internal bending moment varying along the length as:

Substituting into the conservation of energy equation and assuming elastic modulus is constant along the beam:

Example

P = -1000 N

L = 0.1 m

E = 1×10⁹ Pa

t = 0.002 m

h = 0.025 m

Therefore d = -0.0261685 m (the analytical solution).

A Strand7 model of the above is created for comparison:

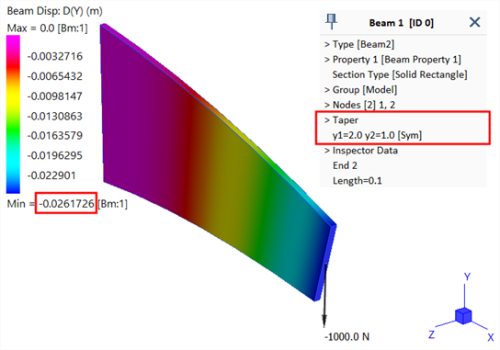
The Strand7 output based on 5 integration points is -0.0261726 m.

The default number of integration points for a beam is 5. By increasing the number of integration points under Common Properties: Sections a convergence study can be undertaken. The results are tabulated below.

Analytical solution			-0.0261685
Strand7	Number of Integration Points	4	-0.0262389
		5	-0.0261726
		6	-0.0261687
		7	-0.0261685
		8	-0.0261685
		9	-0.0261685
		10	-0.0261685